Navigation ... |
|
|
Scientific Writing ... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Other Writing ... |
|
|
|
|
Reference details
| Author(s) | Year | Title | Reference | View/Download |
|---|---|---|---|---|
Les Hatton | 2014d1 | Conservation of Information: Software's Hidden Clockwork ? | IEEE Transactions on Software Engineering, April 2014 | TSE-2013-08-0271_V1.0a.pdf |
Synopsis and invited feedback
This work was or is being reviewed by domain-specific experts appointed independently.
If you would like to provide feedback just e-mail me here.
| Synopsis | Invited Feedback | Importance (/10, author rated :-) ) |
|---|---|---|
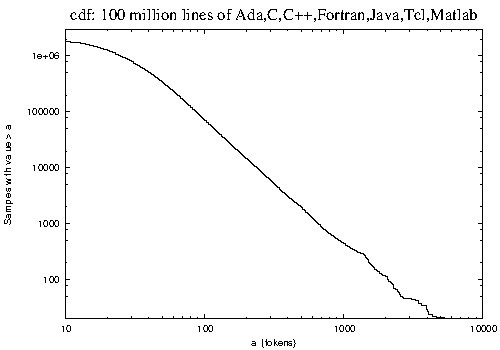
| In this paper it is proposed that the Conservation of Hartley-Shannon Information (hereafter contracted to H-S Information) plays the same role in discrete systems as the Conservation of Energy does in physical systems. In particular, using a variational approach, it is shown that the symmetry of scale-invariance, power-laws and the Conservation of H-S Information are intimately related and lead to the prediction that the component sizes of any software system assembled from components made from discrete tokens always asymptote to a scale-free power-law distribution in the unique alphabet of tokens used to construct each component.
This is then validated to a very high degree of significance on some 100 million lines of software in seven different programming languages independently of how the software was produced, what it does, who produced it or what stage of maturity it has reached. A further implication of the theory presented here is that the average size of components depends only on their unique alphabet, independently of the package they appear in. This too is demonstrated on the main dataset and also on 24 additional Fortran 90 packages. | None yet | 10 |
Related links
| Related papers and links |
|---|
Auto-generated: $Revision: 1.63 $, $Date: 2020/01/25 16:18:09 $, Copyright Les Hatton 2001-